Vertical Circular Motion

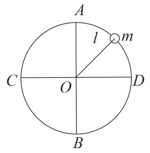
A small sphere is attached to a cord and rotates in a vertical circle about a point $O$. If the range speed of the sphere is increased, the cord is most likely to break at the orientation when the mass is at:

A stone tied to a string is rotated in a vertical circle. The minimum speed of the stone during a complete vertical circular motion 

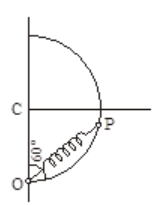
A smooth semicircular wire track of radius $R$ is fixed in a vertical plane One end of a massless spring of natural length  $\frac{\mathrm{}\mathrm{}\mathrm{}3R}{4}$  is attached to the lowest point $O$of the wire track. A small ring of mass $m$ which can slide on the track is attached to the other end of the spring. The ring is held stationary at point $P$ such that the spring makes an angle of  $60°$ with the vertical. The spring constant $K=\frac{mg}{R}$ . Consider the instant when the ring is released. Find the normal reaction on the ring by the track.

A small block is shot into each of the four smooth tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in

If a particle attached to a string is just able to complete a vertical circular motion, then the ratio of the kinetic energy of a particle at the lowest point to that at the highest point is $x:1$. Write the value of $x$.

A point mass $\mathrm{M}$ is hanging by a string of length $\mathrm{l}.$ The velocity $v$ which must be imparted to it in order for it to just barely reach the top is

A pendulum is made of a rigid rod (mass $m,$ length $l$ ) and a small bob of mass $M$ attached at one end (as shown in the figure). The rod is pivoted on the other end. What should be the minimum speed of the bob at its lowest point so that the pendulum completes a full circle ?

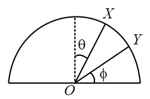
A particle is released on a vertical smooth semicircular track from point $X$ so that, $OX$ makes angle $\mathrm{\theta }$  from the vertical (see figure). The normal reaction of the track on the particle vanishes at the point $Y$ where $OY$ makes an angle $\mathrm{\varphi }$ with the horizontal. Then

The bob of a pendulum of mass $m$ and length $L$ is displaced $90°$ from the vertical and gently released. In order that the string may not break upon passing through the lowest point, its minimum strength must be

A particle of mass $m$ begins to slide down a fixed smooth sphere from the top. What is its tangential acceleration when it breaks off the sphere?

A particle is moving in a vertical circle. The tensions in the string when passing through two positions at angles $30°$ and $60°$ from vertical (lowest positions) are $T_1$ and $T_2$, respectively. Then

A mass $m$ is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break, when

Concrete mixture is made by mixing cement, stone and sand in a rotating cylindrical drum. If the drum rotates too fast, the ingredients remain stuck to the wall of the drum and proper mixing of ingredients does not take place. The maximum rotational speed of the drum in revolutions per minute (rpm) to ensure proper mixing is close to:
(Take the radius of the drum to be $1.25 \mathrm{m}$ and its axle to be horizontal):

A particle is suspended by a light vertical inelastic string of length $l$ from a fixed support. At its equilibrium position, it is projected horizontally with a speed $\sqrt{6gl}$. What is the ratio of the tension in the string in its horizontal position to when the particle is vertically above the point of support?      

A uniform ball of radius $r$ is placed on the top of a sphere of radius $R=10r$. It is given a slight push due to which it starts rolling down the sphere without slipping. The spin angular velocity of the ball when it breaks off from the sphere is $\omega =\sqrt{\frac{p}{q}\left(\frac{g}{r}\right)}$, where $g$ is the acceleration due to gravity and $p$ and $q$ are the smallest integers. What is the value of $p+q$?

A pendulum string of length $𝓁$ moves up to a horizontal position as shown in figure and released.




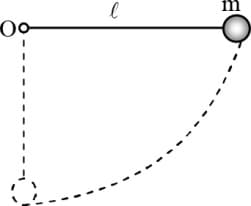
What should be the minimum strength of the string to withstand the tension as the pendulum passes through the position of equilibrium? The mass of the pendulum is $m$.

There is a parabolic bridge across a river of width $10 \mathrm{m}$. The highest point of the bridge is $4 \mathrm{m}$ above the level of the bank. A car of mass $72 \mathrm{kg}$ is crossing the bridge at a constant speed of $5 \mathrm{m} {\mathrm{s}}^{-1}$. Find the force (in Newton) exerted on the bridge by the car when it is at the highest point $P$ of the bridge in newton. (Take, $g=10 \mathrm{m} {\mathrm{s}}^{-2}$.)

A particle is tied to a string describes a vertical circular motion of radius $r$ continually. If it has a velocity $\sqrt{3gr}$ at the highest point, then the ratio of the respective tensions in the string holding it at the highest and lowest points is

If a stone of mass $2 \mathrm{kg}$ Is tied to an inextensible string of length $2 \mathrm{m}$ Is whirling in a circular path of radius $L$ In vertical plane at uniform speed. If the ratio of maximum tension to minimum tension in the string is $3.$If, the speed of stone at highest point of circle is $6.3x \mathrm{m} {\mathrm{s}}^{-1}$ then find $x$.